[Python] Rot-13 Encryption Method

If he had anything confidential to say, he wrote it in cipher, that is, by so changing the order of the letters of the alphabet, that not a word could be made out. If anyone wishes to decipher these, and get at their meaning, he must substitute the fourth letter of the alphabet, namely D, for A, and so with the others.

Suetonius, Life of Julius Caesar

Foto von Rachel Claire von Pexels

The ROT-13 (i.e. rotate by 13 places) method is a very simple encryption method, in which one replaces each letter of the alphabet with the 13^th letter after it. So, ‘A’ becomes ‘N’, ‘B’ becomes ‘M’ and so on. This method is a special case of the Caesar Cipher, with which Caesar encoded his letters in the ancient Rome.

Let’s write some simple code that can encode and decode given text files based on the ROT-13 method in Python!

Here is our approach for encoding a given string:

First, all the letters of the given text are transformed to lower case letters.
Then we loop through all characters, and if the character is a letter, we replace it with the 13^th letter after it. If it is not a letter (for instance ‘?’), we just add it to the final solution.

Bear in mind that, after ‘z’ we start counting from ‘a’ again: for instance, ‘n’ is the 14^th letter of the alphabet, so if we use ROT-13 on it, we arrive at 27, which is one after ‘z’, or ‘a’, and to do so in our code, we always consider the remainder of any number divided by 26. In our example the remainder of dividing 27 by 26 is 1, which is ‘a’.

We can write a function to decode the given string, but wait! There are 26 (2 * 13) letters in the alphabet, so ROT-13 is basically it’s own inverse. In other words: ROT13(ROT13(x)) = x.

Let’s jump to the code:

Copy Code


"""Econowmics.com"""

# Rot 13

# The alphabet
alphabet = 'abcdefghijklmnopqrstuvwxyz'

# Function to encrypt a text based on the Rot-13 method
def encrypt(text):
    """The function receives a string as input, and encrypts it using the Rot-13 method """
    
    # Transform the string to lower-case chars
    text = text.lower()
    
    # the encrypted message
    result = ''
    
    # Replace each letter in the string with a letter which is 13 positions further
    for char in text:
        if char.isalpha():
            result += alphabet[(alphabet.index(char) + 13) % 26]
        else:
            result += char
    return result
        

# Function to decrypt a text based on the Rot-13 method
def decrypt(text):
    """The function receives a string as input, and decrypts it using the Rot-13 method """
    
    # Transform the string to lower-case chars
    text = text.lower()
    
    # the decrypted message
    result = ''
    
    # Replace each letter in the string with a letter which is 13 positions backwards
    for char in text:
        if char.isalpha():
            # the new position
            position = alphabet.index(char) - 13
            if position < 0:
                result += alphabet[26 + position]
            else:
                result += alphabet[position]
        else:
            result += char
    return result

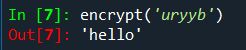
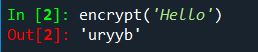
So, let’s try encoding a simple ‘Hello’:

ROT13 - Encryption Test - Econowmics.com