[Python] Number Spirals

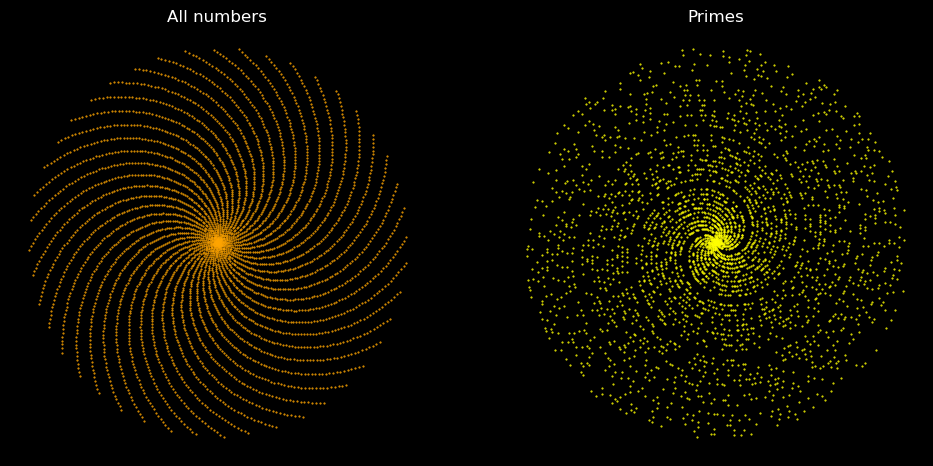
The patterns in a nutshell

Recently I watched a video on 3Blue1Brown Youtube Channel about a specific patten that would emerge as a result of plotting points with similar polar coordinates (r, θ), i.e. those points for which r and θ are the same. To find more information about it you can watch the video here.

You can find the codes here:

Copy Code


# Youtube: @Coded Abacus
# Econowmics.com

# libraries
import matplotlib.pyplot as plt    # plotting
from math import sin, cos          # Cartesian coordinates

# define the graph style
plt.style.use('dark_background')

# import the list of primes
f = open(r'primes.txt', 'r')

# read in the primes and create a list out of them
lines = f.readlines()
primes = [int(x) for x in lines[0].split(',')]

# total points 
n = 80000

# prepare the lists
p = primes[:n]
nums = list(range(1, n+1))

# function to convert polar coordinates to cartesian
def p_to_c(lst):
    x_c = [i * cos(i) for i in lst]
    y_c = [i * sin(i) for i in lst]
    
    return x_c, y_c

# Plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (10, 5))

# plot all numbers on the left subplot
n_x, n_y = p_to_c(nums)
ax1.scatter(n_x, n_y, s = 0.6, color = 'orange')
ax1.set_title('All numbers')

# plot the primes on the right subplot
p_x, p_y = p_to_c(p)
ax2.scatter(p_x, p_y, s = 0.6, color = 'yellow')
ax2.set_title('Primes')

# adjust the spacing
plt.tight_layout()

# no axis
ax1.axis('off')
ax2.axis('off')

# display the figure
plt.show()

To find more information and see the step by step implementation you can watch this video: