[Python] Prime number generator

God may not play dice with the universe, but something strange is going on with the prime numbers.

Paul Erdos

Photo by Markus Spiske from Pexels

A prime number is a positive number greater than 1, which has no positive integer divisors except 1 and itself. Therefore, numbers like 2, 3, 5, 7, 11 are all prime numbers.

As a result of the definition of a prime number, one might probably decide to check if a given number, x, is prime by trying to divide it by all the integers starting from 2 and smaller than x. If no such number divides x evenly, then it can be concluded that x is a prime number. Although such a method can be used for very small numbers, but it will be very time consuming and also subject to errors for large numbers. For instance, if x=100,000,000, then the program must check each and every number between 2 and 99,999,999 to see if it divides x evenly or not.

Better methods can nevertheless be used to calculate prime numbers. One of the most efficient algorithms for calculating prime numbers is called Sieve of Eratosthenes. Put simply, this algorithm starts from the very first prime number, 2, and marks every multiple of it smaller than x as composite. Then the algorithm continues with the next prime number. The remaining numbers will be primes. The following animation, adapted from Wikipedia, clearly illustrates this algorithm.

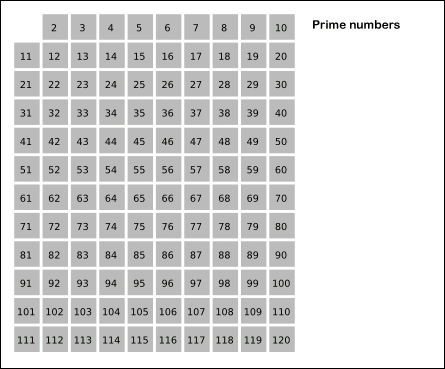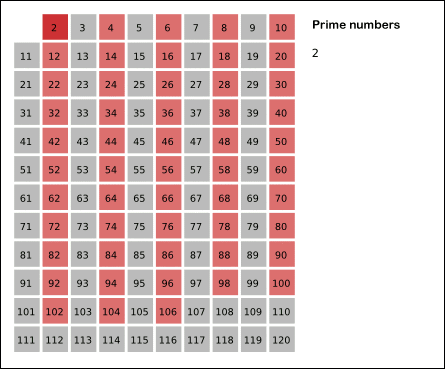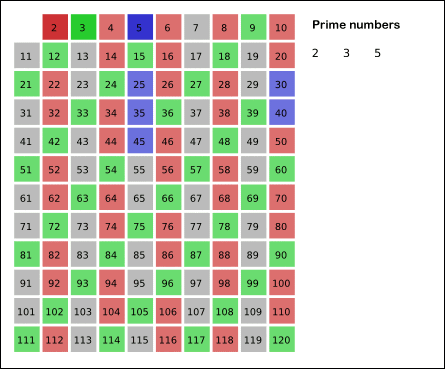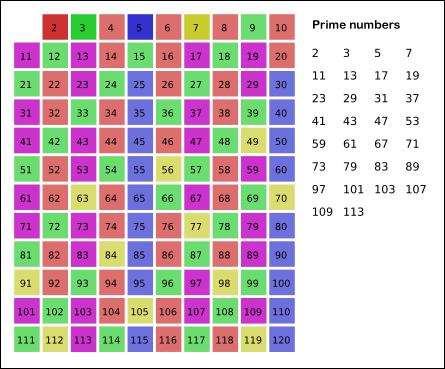
prime number calculation method

Let’s have a quick look at the code which does this for us:

Copy Code


"""Econowmics.com"""

def Sieve(n):
    """This function calculates all prime numbers up to a given limit(n)"""
   
    #Defining the inintial list, all equal to True
    primes = [True for i in range(n+1)]
    primes [0] = primes [1] = False

    #The starting number
    p = 2

    #Running a loop to check all numbers below the square root of the given number
    while p ** 2 < n:
        #Check to see if it is equal to True (if the number is prime or not)
        if primes[p]:
            #If it was a prime number, kill every other multiple of it
            for number in range(p*2, n+1, p):
                primes[number] = False

        #Increment the starting number by one to keep the loop working
        p += 1 

    prime_numbers = [i for i in range (n+1) if primes[i]==True]
    #If you want to see the list of prime numbers in the output
    #return prime_numbers

    #If you want to see how many prime numbers are there in a given range
    return len(prime_numbers)



import time

#marking the starting time
start = time.time()

#For-loop to evaluate the function
for i in [10,100,1000,10000,100000,1000000,10000000,100000000]:
    print ("There are " + str(Sieve(i)) + " prime numbers below " + str(i) + ".")

#marking the end of time and calculating the total duration  
end = time.time()
duration = end - start
print (duration)

First, we define a list equal to the size of n, with all elements equal to True. As the algorithm runs, those indexes of this list that are marked as composite will be changed to False. Before the loop, we set the first two instances, namely 0 and 1, which are not primes, into False.

Then, we define the starting number, p=2.

In the next step, we start a loop to check all the numbers below the square root of the number we are looking for. The reason why we only check the numbers below the square root can be seen from this photo:

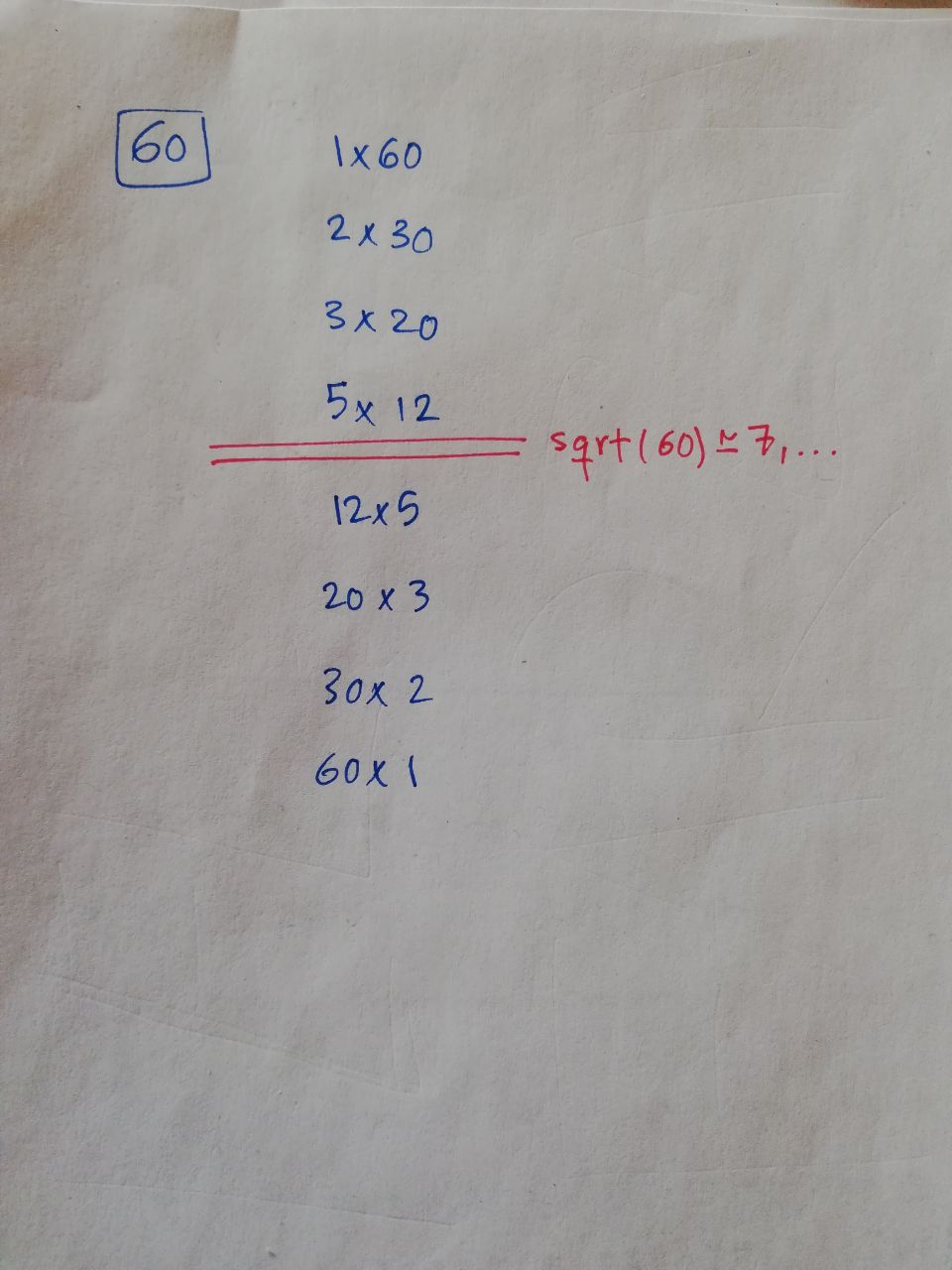
The factors repeat themselves after the square root of the given number.

After the square root, the numbers just repeat themselves and it would be of no use to check the other numbers.

Now, if the number in the index that we are checking is actually a prime, we set all of its multiples as composite, i.e. set them to False (not primes).

Then we increment p by 1 to check the next number. This goes on until the condition of the while-loop turns False.

In the last step, we can return the result that we want. For example, here two options are given. Depending on each one suits you best, you have to uncomment it. Here, we check for the total amount of primes less than a given number.

Let’s test the function:

[pastacode lang=”python” manual=”import%20time%0A%0A%23marking%20the%20starting%20time%0Astart%20%3D%20time.time()%0A%0A%23For-loop%20to%20evaluate%20the%20function%0Afor%20i%20in%20%5B10%2C100%2C1000%2C10000%2C100000%2C1000000%2C10000000%2C100000000%5D%3A%0A%20%20%20%20print%20(%22There%20are%20%22%20%2B%20str(Sieve(i))%20%2B%20%22%20prime%20numbers%20below%20%22%20%2B%20str(i)%20%2B%20%22.%22)%0A%0A%23marking%20the%20end%20of%20time%20and%20calculating%20the%20total%20duration%20%20%0Aend%20%3D%20time.time()%0Aduration%20%3D%20end%20-%20start%0Aprint%20(duration)” message=”” highlight=”” provider=”manual”/]

Which results in:

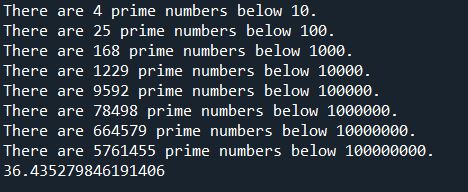
prime number calculation result

[Python] Prime number generator

Also watch

Further reading on prime numbers

Related posts: