[Kattis] Stirling’s Approximation

Stirling’s grave in Greyfriars Kirkyard, Edinburgh (Source: Wikipedia)

Stirling’s approximation is a powerful mathematical formula which can be used to estimate the value of N!, and it is especially handy when it comes to large values of N. It was derived by the the French mathematician Abraham de Moivre (1667-1754) and the Scottish mathematician James Stirling (1692-1770). The approximation is given by this formula:

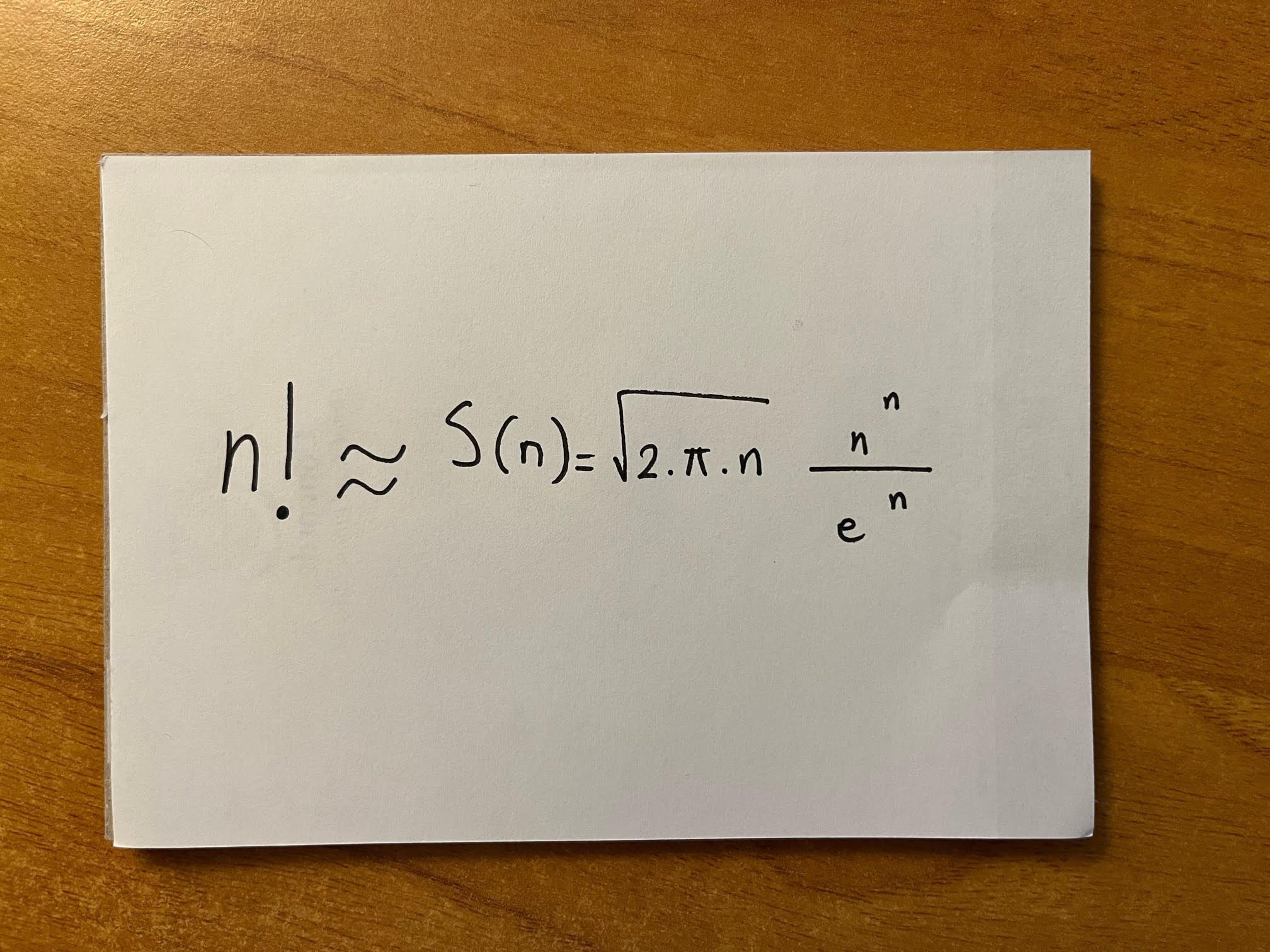
Stirling’s approximation formula

where π is roughly equal to 3.14, and e (the Euler’s number) is roughly equal to 2.718.

Stirling’s approximation is an invaluable tool in various fields, including statistics, physics, and engineering, where large factorials frequently arise. It becomes even more accurate as N increases.

This post is associated with a programming puzzle from Kattis. Here you can find more about the puzzle and its solution:

And here you will find the code for the solution:

# Libraries
from math import log, pi, e

# function to calculate the logarithm of S(n)
def log_sn(n):
    return 0.5 * (log(2) + log(pi) + log(n)) + n * (log(n) - log(e))

# function to calculate the logarithm of the factorial
def log_fact(n):
    return sum(log(i) for i in range(2, n+1))

# The puzzle
while True:
    # receive n
    n = int(input())
    
    # the exit condition
    if n == 0:
        break
        
    else:
        print(e ** (log_fact(n) - log_sn(n))

Related Images: