[Python] Pandigital numbers

Numbers do not feel. Do not bleed or weep or hope. They do not know bravery or sacrifice. Love and allegiance. At the very apex of callousness, you will find only ones and zeros.

Amie Kaufman, Illuminae

Photo by Pixabay from Pexels

A pandigital number is a number that contains each digit starting from one, up to the total length of the number. For instance, 15342 is a pandigital number, since it has all the digits starting from zero up to the total length of the number, which is 5. On the contrary, 4433 is not a pandigital number, since it does not have 1 and 2 among its digits.

Bear in mind that some definitions of pandigital numbers start from 0 instead of 1. The functions that we consider here take care of the definition given in the above paragraph, but they are easily modifiable to be implementable by the other definition as well.

Three methods are offered to check if a given number is in fact pandigital or not. They are basically very similar to each other, and only differ in their performance and efficiency.

Method 1

#The first function
def pandigital1(n):
    
    #Turn the number into string
    number = str(n)
    
    #Empty list to store the digits of the number
    digits = []
    
    #Go through each digit of the number and check if it is repetitive or not
    for digit in number:
        #If the digit already exists in the digits list, then this number is not pandigital
        if digit in digits:
            return False
        #Otherwise, add the digit to the digits list
        else:
            digits.append(digit)
    
    #What we expect, by the definition of a pandigit number        
    goal = [str(x) for x in range(1, len(number)+1)] # goal = [1, 2, ...., len(number)]
    
    #If the sorted list of digits is equal to what we want, then it is a pandigital number
    if goal == sorted(digits):
        return True
    else:
        return False

1. In this algorithm, we first take the number and turn it into string.
2. Then we loop through the elements of this string, and if these elements are not repetitive, we add them to a pre-defined empty list
3. We also define what we expect from a pandigital number. This step is the same in all of these methods. So, for example, if we have a 5-digit number, we expect that its sorted digits are of the form: [1, 2, 3, 4, 5]. Starting from 1 and ending at the length of the number, which is 5 here.
4. At a final step, we check if these two lists are the same: If so, then it is a pandigital number.

Method 2

#The second function
def pandigital2(number):
    """This function checks if a number can be written as a 1 through 9 pandigital."""
    
    #I begin by changing the data type to string
    number = str(number)
    #Then I sort the digits in the number
    number = sorted(number)
    
    #Now I create a list of the digits starting from 1 until the length of the given number
    digits = [str(x) for x in range(1, len(number)+1)]
    
    #Now I check if the two are the same
    if number == digits:
        return True
    else:
        return False

1. Here again, we start by receiving the number and turning it into the string.
2. But we do not loop through each and every digit again, rather we just sort the string that we obtained in the previous step.

The last two steps are exactly the same as the previous method.

Method 3

#The third function
def pandigital3(n):
    #Turn the number into a string
    number = str(n)
    #What we expect, by the definition of a pandigit number 
    digits = [str(x) for x in range(1, len(number)+1)]
    #Check if the two are the same
    return set(number) == set(digits)

This one is very similar to the second method. Instead of sorting the number, we just turn it into a set. A set cannot have repetitive numbers, so it helps shorten the code.

Comparison

Let’s check how these functions can be ranked based on performance and efficiency. I guess it is going to be a tight match.

I check how many numbers each of these function find for numbers below 1,000,000, so that we can be sure that the functions are working properly. And I also check how much does it take for each function to do the job.

Here is the result:

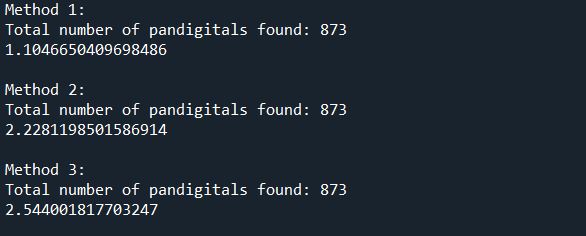
As it turns out, all the three functions are working properly as they all found 873 pandigital numbers below 1,000,000. Nevertheless, the first function is the fastest of them all, needing about half the time that the two other function need to process all the data.